How To Find F Prime

The Notation of Differentiation

Suggested Prerequesites: The definition of the derivative

Often the most confusing affair for a educatee introduced to differentiation is the note associated with it. Here an attempt volition be made to innovate as many types of notation as possible.

A derivative is always the derivative of a function with respect to a variable. When we write the definition of the derivative as

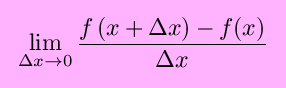
we mean the derivative of the function f(x) with respect to the variable 10.

One type of annotation for derivatives is sometimes called prime annotation. The function f´(x), which would exist read ``f-prime number of ten'', means the derivative of f(x) with respect to x. If we say y = f(ten), then y´ (read ``y-prime'') = f´(10). This is even sometimes taken as far every bit to write things such as, for y =x ⁴ + 3x (for example), y´ = (x ^iv + 3x)´.
Higher order derivatives in prime note are represented by increasing the number of primes. For example, the second derivative of y with respect to 10 would exist written as

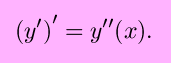
Across the 2nd or third derivative, all those primes get messy, so often the order of the derivative is instead writen as a roman superscript in parenthesis, so that the 9th derivative of f(x) with respect to x is written equally f ⁽⁹⁾(x) or f ^(ix)(x).

A second type of annotation for derivatives is sometimes chosen operator note. The operator D _x is applied to a function in guild to perform differentiation. Then, the derivative of f(10) =y with respect to ten tin exist written as D_xy (read ``D -- sub -- x of y'') or as D_xf(x (read ``D -- sub ten -- of -- f(ten)'').

College order derivatives are written past adding a superscript to D₁₀ , and so that, for example the third derivative of y = (x ²+sin(x)) with respect to x would be written every bit

Another ordinarily used notation was adult by Leibnitz and is accordingly called Leibnitz note. With this notation, if y =f(x), and then the derivative of y with respect to x can be written equally

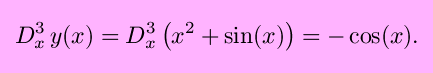
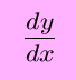
(his is read equally ``dy -- dx'', but not ``dy minus dx'' or sometimes ``dy over dx''). Since y =f(x), we tin also write

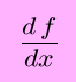
This notation suggests that perchance derivatives can be treated like fractions, which is true in limited ways in some circumstances. (For example with the chain rule.) This is also called differential note, where dy and dx are differentials. This notation becomes very useful when dealing with differential equations.

A variation of Leibnitz'due south differential notation is written instead as

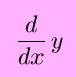
which resembles the above operator notation, with (d/dx as the operator).

College order derivatives using leibnitz notation can be written every bit

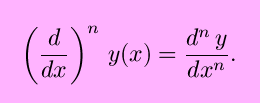
The exponents may seem to exist in strange places in the second form, just it makes sense if you wait at the beginning class.

And so, those are the nearly usually used notations for differentiation. It's possible that there exist other, obscure notations used by a some, but these obscure forms won't be included here. It'due south helpful to be familiar with the different notations.

When is a function differentiable?

Back to the Calculus folio | Back to the World Web Math top page

watko@mit.edu

Last updated August 24, 1998 <\body>